MHB Winning Tennis with Probability 0.3 and 0.7

Hi,

What is your probability of winning a game of tennis, starting from the even score Deuce (40-40), if your probability of winning each point is 0.3 and your opponent’s is 0.7?



My answer:
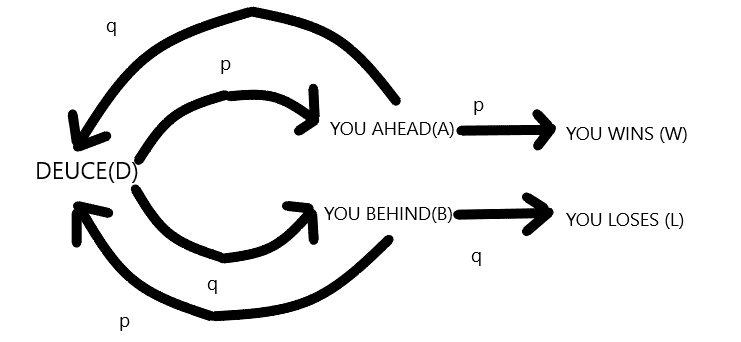
I think the sequence of independent trials are required to win a game of tennis starting from even score Deuce(40-40),each of which is a success with probability (0.3 × 0.3 =0.09) or a failure with probability (0.7 × 0.3 + 0.7 × 0.3 =0.42). Suppose, the independent trials to win a game of tennis are n. That means after (n-1) trials of failures, the nth trial is success.

$$ \displaystyle\sum_{n=0}^{\infty} 0.09 \cdot (0.42)^n =\lim_{n \to \infty}\frac{0.09\cdot ( 1 - 0.42^n)}{1- 0.42}= 0.15517 $$ = 15.51 %

Have you worked out the states and the state transition probability matrix?
I see the states as
Deuce, Ad-In, Ad-Out, Game

with Game being an absorbing state.

Write out all the conditional probabilites P(W|X) where X = A, B, D. You will have a linear system of three unknowns and three equations, which can be solved by standard methods.

For example: If you are in state B, you must win the next point to have any chance of winning. If you lose the point you lose the game, so
P(W|B) = q P(W|D)
because if you do win the point (which you do with probability q), then you will be in state D and your probability of winning will be P(W|D).

There is a useful shortcut in considering two point played at a time. If the probability of winning a point is ##p##, then the probability of winning the game (##P##) satisfies:
$$P = p^2 + 2p(1-p)P$$Hence$$P = \frac{p^2}{2p^2 - 2p + 1}$$With ##p = 0.3##, this gives ##P \approx 0.155##.

PeroK said:

There is a useful shortcut in considering two point played at a time. If the probability of winning a point is ##p##, then the probability of winning the game (##P##) satisfies:
$$P = p^2 + 2p(1-p)P$$Hence$$P = \frac{p^2}{2p^2 - 2p + 1}$$With ##p = 0.3##, this gives ##P \approx 0.155##.

Other way of seeing this: Probability of winning in two points is ##p^2##. Probability of losing in two points is ##(1-p)^2 = 1-2p+p^2##. Probability of winning must therefore be
\[
\frac{p^2}{p^2 + (1-p)^2} = \frac{p^2}{2p(p-1) + 1}
\]
as otherwise we return to the same state.